√完了しました！ 階差数列の和の求め方 247312-階差数列の和の求め方

 階差数列\( \{ b_n \} \)の和が求められるなら、元の数列\( \{ a_n \} \)の一般項が求められる ということを、逆に見ればわかります。 階差数列\( \{ b_n \} \)の和は、\( a_{n1} – a_1 \)で計算できる まず、和を求めたい数列を\( \{ b_n \} \)としましょう。 では、等比数列の一般項の求め方と、和の公式がわかったところで、大学入試でよく出る応用問題を解いていきましょう。 漸化式の問題で等比数列は頻出 漸化式の問題では、等比数列は頻出です。 問題次の漸化式で定義される数列{an}の一般項を求めよ。 5anのように、項の前に定数階差数列の和の考えを逆利用した数列の和の求め方 数列 {a_n}の一般項a_nは, n≥2のとき, この数列 {a_n}の階差数列 {b_n}を用いて, 公式a_n=a_1Σ^^__b_kから求められる場合がある。その場合, 重要なことはb_kが分かっていることであるが, この考え方を発展

48s96ub7b0z5f Net Tousa Suuretsu

階差数列の和の求め方

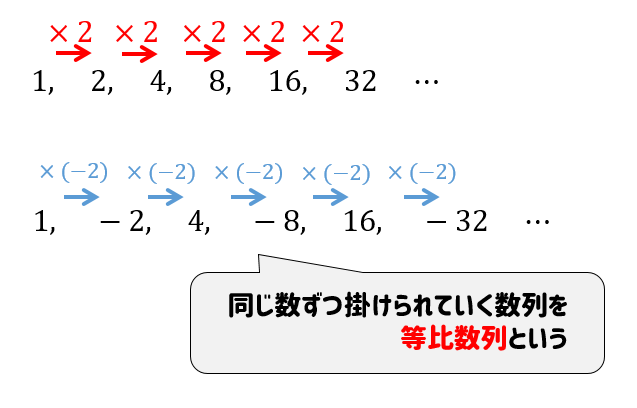
階差数列の和の求め方- Σシグマの計算方法や公式を忘れてしまった人は「 Σシグマの公式まとめと計算方法（数列の和の公式） 」の記事で詳しく解説しているので，チェックしておきましょう。 階差数列を用いて，なぜもとの数列が「 \displaystyle \color {red} { a_n = a_1 \sum_ {k=1}^ {n1} b_k } 」と表すことができるのか、導出をしていきましょう。 以上のようにして公式を得ることができます 初項が a a a ，末項が l l l ，項数が n n n であるような等差数列の和は， 1 2 n (a l) \dfrac{1}{2}n(al) 2 1 n (a l) →等差数列の和の公式の例題と証明など 等比数列 例： 1 2 4 8 16 = 31 =31 1 2 4 8 16 = 31 初項が a a a ，公比 r r r ，項数 n n n の等比数列の和

階差数列とは 和の公式や一般項の求め方 漸化式の解き方 受験辞典

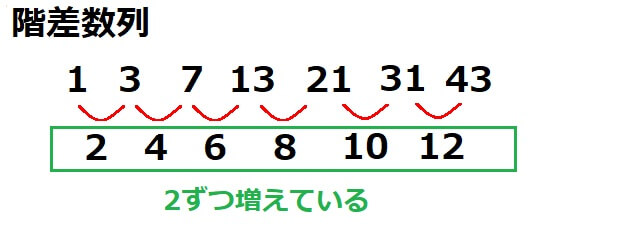
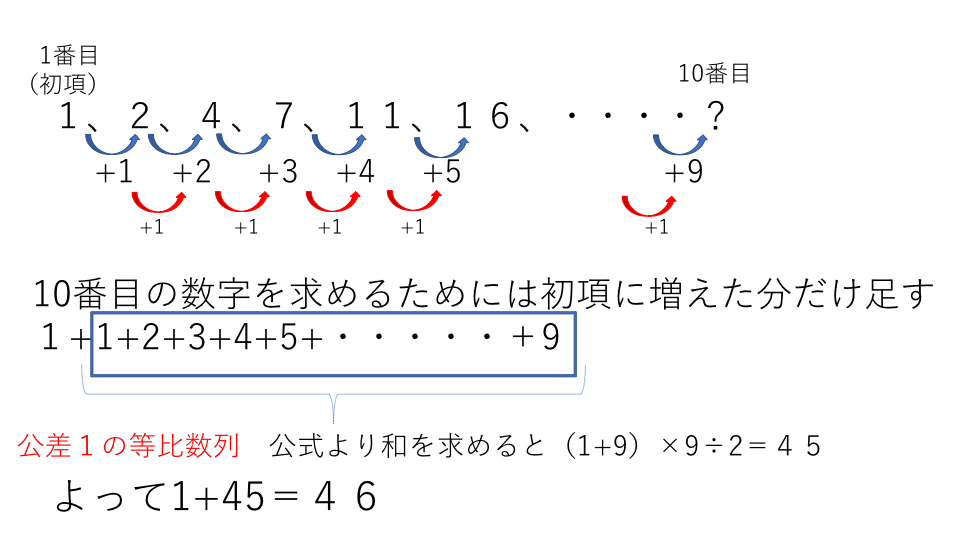
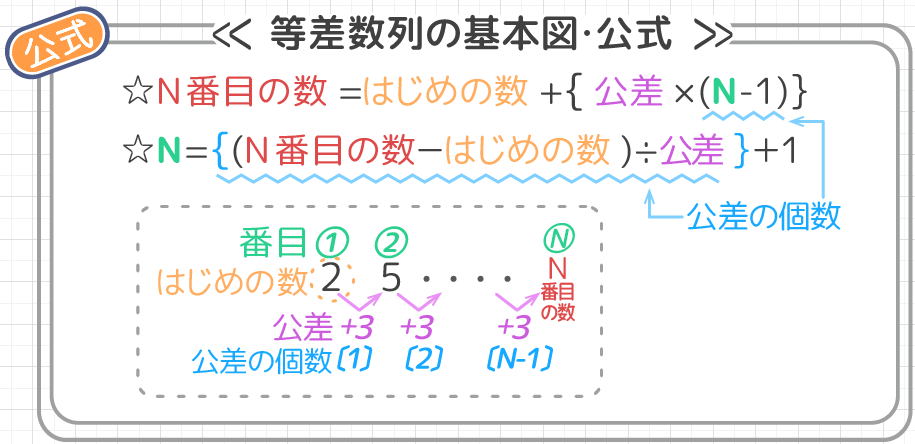
 先程の考え方を使うと、 Aの10番目の数＝Aのはじめの数＋Bの9番目までの和 です。 まず「Aのはじめの数」は 2 です。 次に「Bの9番目までの和」を求めます。 等差数列の和の公式 (はじめの数＋N番目の数) N÷2 をB1,2,3,4にあてはめると、「はじめの数」=1,「9番目の数」=9「N」=9なので 「Bの9番目までの和」＝ (1＋9) 9÷2＝ 45 になります。 以上より、 Aのはじめの数=2この記事では、「階差数列」の意味や公式（階差数列の和を使った一般項の求め方）についてわかりやすく解説していきます。 漸化式の解き方なども説明していくので、この記事を通してぜひマスターしてくださいね！ 数学における等差数列（とうさすうれつ、英 arithmetic progression, arithmetic 階差数列 階差数列とは、 各項の差が数列のようになっている数列 のことを言います。 例えば 2、3、5、8、12、 このような数列のことです。一見規則性が無いように思われますが、2から3は＋1、3から5は＋2、5から8は＋3、8から12 は＋4となっています。このように差に数列のように規則性があるものを階差数列と呼びます。

☆等差数列の和を計算するプログラムを作 る。 2 10年度プログラミング演習資料 第7回繰り返しⅡ（回数による繰り返し） for文 条件式（論理式）が真である間、命令を繰り返し実行する。 書式 for(式1;条件式;式2) {反復実行部分 for文のフローチャート for文前} 式1； for文 反復実行部分条件式の 階差数列とは？ 和の公式や一般項の求め方、漸化式の解き方 21年2月19日 この記事では、「階差数列」の意味や公式（階差数列の和を使った一般項の求め方）についてわかりやすく解説していきます。 漸化式の解き方なども説明していくので、この記事を通してぜひマスターしてくださいね！ 目次 非表示 階差数列とは？ 階差数列と一般項の公式 一般項の元の数列を｛ａ ｎ ｝，階差数列を｛ｂ ｎ ｝とおくと，｛ｂ ｎ ｝は １，４，９，１６，２５・・・ ｂ ｎ = ［ア］ n≧2のとき， これはn=1のときも成り立つ。

実際に数字を使って和を求めてみましょう。 階差数列の和を求める このような数列があったとします。 1 , 3 , 7 , 13 , 21 , 31 , 43 この数列の階差数列は「初項2、公差2の等差数列」です。ここで，初項 3，公差 2，項数 10 の等差数列 3，5，7，9，11，13，15，17，19，21 を考え，その和を求めてみましょう。皆さんはどのようにして求めますか？ いろいろな求め方がありますが，ここでは，次のようにして求めることにします。 今，求める和を s よって階差数列の式に代入すると欲しい数列の一般項は、 n ≥ 2 のとき a n = a 1 ∑ k = 1 n − 1 2 k 3 = 6 2 ∑ k = 1 n − 1 k 3 ∑ k = 1 n − 1 1 = 6 2 ⋅ 1 2 ( n − 1) n 3 ( n − 1) = 6 n 2 − n 3 n − 3 = n 2 2 n 3 と計算できるわけです。 シグマ記号一番最後が n − 1 であることに十分注意してください！ ！ そして最後に、今求めた一般項がもともとの数列の初項を

等差数列 等比数列の解き方 階差数列 漸化式をスタサプ講師がわかりやすく解説 ガジェット通信 Getnews

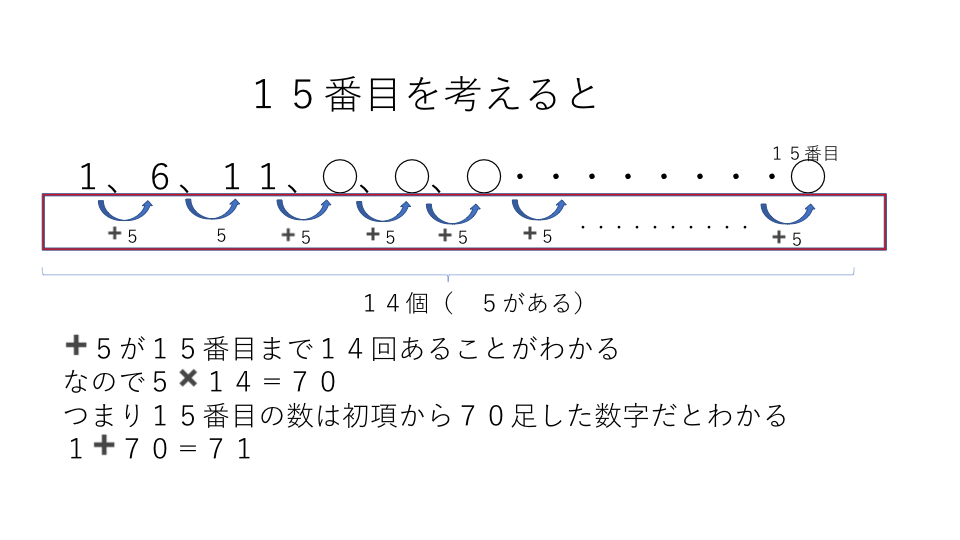
中学受験 算数 等差数列 等比数列 階差数列の重点ポイントまとめ 中学受験アンサー

 あくまで階差数列とは数列\( \{ a_{n1} a_n \} \)のことです。出題されるものはこれに規則性があるというだけです。 階差数列を用いた一般項の計算 階差数列とは何か分かったところで実際にこれを用いて複雑な数列の一般項を求めてみましょう。 \( 1, 7, 18, 34それはこの数列の分け目をはずしたときの一般項を考えればすぐ分かる。この数列は群の分け目をはずせば，初項1，公差3の単純な等差数列で，その第k項は となるから，第86項であれば と計算できる。（一般項 を求めずに，直接 と計算しても良い。等比数列の一般項は？1分でわかる求め方、和の計算、等差数列との違い 等差数列の公式は？3分でわかる公式、覚え方、等差数列の和の計算 無料自己分析あなたの本当の強みを知りたくないですか？⇒ 就活や転職で役立つリクナビのグッドポイント診断 数列とは？ 数列（すうれつ）と

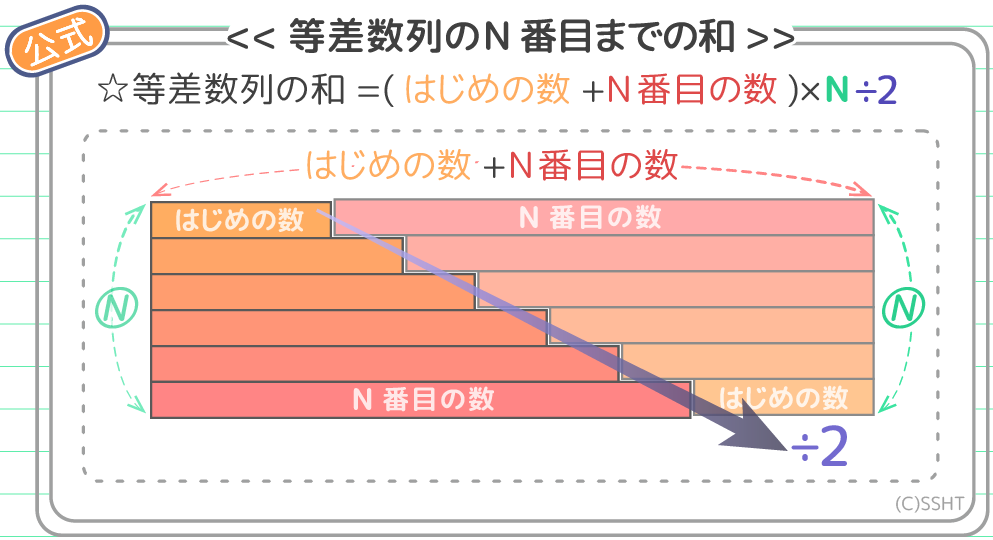
中学受験 差 階差数列 を利用する問題の解き方 無料プリントあり そうちゃ式 受験算数 新1号館

等差数列をグラフにしてみよう 父ちゃんが教えたるっ

 ちなみに、三角数の和を公式化すると、 \(\displaystyle S_n=\frac{ 1 }{ 6 } n ( n 1 ) ( n 2 )\) あれ？ どっかで見たような \(\displaystyle \sum_{ k = 1 }^{ n } k^2 =\frac{ 1 }{ 6 } n ( n 1 ) ( 2n 1 )\) \((=1^2 2^2 \cdots n^2)\) ああ！ 平方数の和の公式とクリソツ。 平方数の和に関しても、先ほど三角数の和を導き出したやり方と同じようにできるのです。3．階差数列 前の項と次の項の差に明らかな特徴がある （例）2,3,5,8,12, ‥‥ 4．その他（漸化式） その他の一般項の求め方はこちらで説明しています。 漸化式の求め方 それでは問題を解いていき の和を階差数列の考え方を使って求めていきたいと思います。 和を求めるのに必要なものは 階差数列がnとなるような、nの2次式で表される数列 です。 つまり \ a_{n1} – a_n = n \ となる2次式で表される数列\( \{ a_n \} \)を求めることができれば、1からnまでの和を求めることができる

48s96ub7b0z5f Net Tousa Suuretsu

等比数列の公式まとめ 一般項 和の公式 証明 理系ラボ

階差数列について理解し，知識を身に付け る。また，階差数列を利用して数列の規則性を の初項から第n項までの和の求め方を振り返る ことで，その考え方が応用できないか問いかけ る。 〔数学的な見方や 考え方①〕 （ワークシート） 4 3 2で考察した方法 で、数列 {n(n＋1)(n＋2)} の和階差数列とは の階差数列といいます。 つまり、隣同士の差をとったときにあらわれる数列のことです。 （ ）内は第1項から第（n1)項までの和である。これをΣ記号を使って表すと Σの計算の仕方 階差数列とは 階差数列とは、ある数列において隣り合う項どうしの差を並べた数列のことをいう。 例えば、1，4，8，13，19 という数列で、それぞれ、4から1、8から4、13から8、19から13 を引いた答えで数列を作ると、3，4，5，6 のようになる。これを階差数列という。

高校数学b 階差を利用する和 連続整数の積の和 Sk K 1 K 2 受験の月

等比数列まとめ 和の公式の証明や一般項の求め方を解説 応用問題つき Studyplus スタディプラス

級数の和と一般項の求め方 ∑k Σk (k1) Σk (k1) (k2) ∑の計算 ΣΣk=136 五角数等差×等比型の和 等比数列，循環数列 群数列 自然数の累乗の和 → 携帯版は別頁 数列の「各項の差」からなる数列を元の数列の階差数列と言います。 例 元の数列よりもその差から作った階差数列の方が簡単な規則性を持っていることが多いので，階差数列で規則性を見つけて，元の数列の一般項を求めることができます。 階差数列の定義 元の数列を { a nS の求め方 「階差0項数列」を使って、数列の一般項を簡単に求める方法 林邦英様 2 3 を苦心して求めていたのですが、こんな簡単な方法があるとは知りませんでした。ただ、私は理解するのが遅くて、わかるまで一週間も かかってしまいました。でも、とても面白いテーマで十分に楽しむ

階差数列を用いて一般項を求める方法について 高校数学の美しい物語

階差数列とは 和の公式や一般項の求め方 漸化式の解き方 受験辞典

⇒ シグマ（Σ）の計算公式が使える数列の和の求め方 （1）で求めた数列 \( \displaystyle a_k=\displaystyle \frac{1}{2}(k^25k2)\hspace{10pt}(k≧ 1) \) の第 \(n\) 項までの「和」です。 数列 \( \{a_k\}\) はどのような数列か分かりません。ログラムを実行するよりOctave 上で処理する方が高速である場合が多い。 練習問題 適当な行列A,B をつくって上のプログラムmat1(A,B) とOctave での行列の積 AB の結果を比較せよ。 32 数列再び 再び数列に話をもどす。数列とは、ある規則に則って求められた数の並びのこと である。ここでいう規則 = AnB タイプ→等差数列だからすぐに一般項が分かる a_n=An^2BnC an = An2 Bn C タイプ→階差数列が等差数列になる a_n=An^3Bn^2CnD an

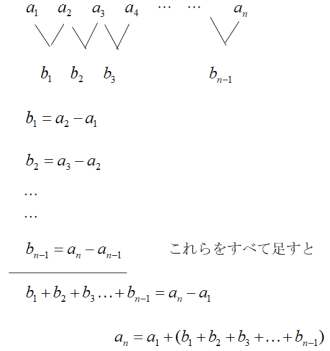
階差数列の解き方 高校生 数学 公式 家庭教師のアルファ プロ講師による高品質指導

階差数列の一般項の求め方を教えて下さい 1 An 1 2 5 14 Yahoo 知恵袋

 階差数列の和が等比になった場合には？ それでは、階差数列の問題を極めるため こちらの問題に挑戦してみましょう！ 次の数列の一般項を求めよ。 $$3, 5, 11, 29, , 245, \cdots$$ こちらも階差数列を使った問題となります。 今回は 階差数列が、等比数列 となっております。 この場合 「等差数列の和」というのは 数列の「はじめの数」から何番目かの数までを全部足したもの です。 例えば「2,5,8という数列の1番目から5番目までの和」なら、「2,5,8,11,14」を合計して=40 となります。 数列の基本6｜部分分数分解を用いて計算する数列の和 部分分数分解を使うことで求めることのできる数列の和があります． 部分分数分解はマイナーな知識と思われがちですが，教科書に載っている基本的な知識ですし，数IIIでは 部分分数分解が必要

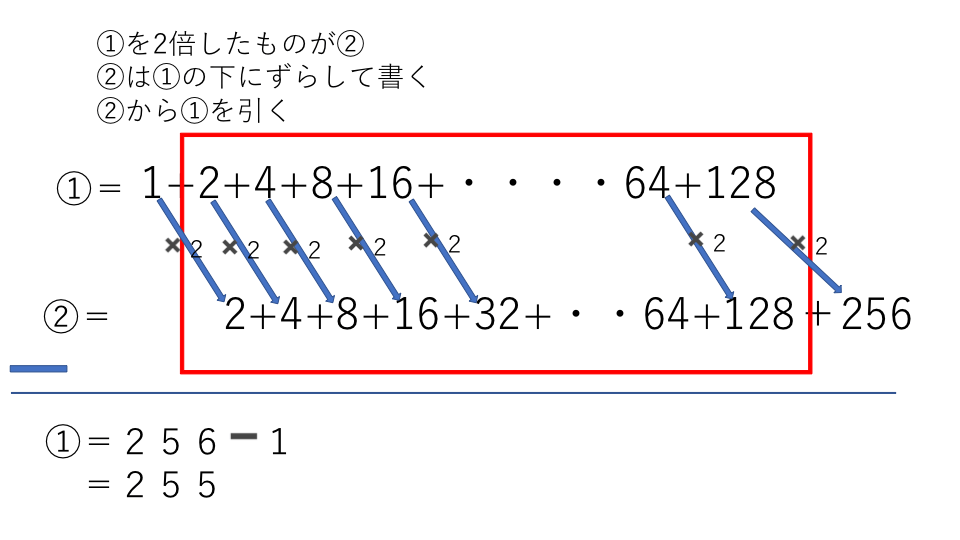
中学受験 算数 等差数列 等比数列 階差数列の重点ポイントまとめ 中学受験アンサー

特殊な和の求め方その２ 等差 等比編 高校数学の知識庫

 このように等比数列の和に公比を掛けた式をつくり、それぞれを引くことによって導くことができます。 また、等比数列の和の公式には $$S_n=\frac{a(1r^n)}{1r}=\frac{a(r^n1)}{r1}$$ このように2パターンあります。階差型の数列 タイプ： 教科書範囲 レベル： ★★ 階差数列を用いて一般項を求める方法について解説します． 当サイトではそのような数列を階差型の数列と呼ぶことにし，深く内容を考察，解説し，演習問題まで用意しました． 目次 1： 階差型の数列 こんにちは。 da Vinch (@mathsouko_vinch)です。 群数列とはここでは群数列について考えていきます。大多数が群数列について間違った捉え方をしていると管理人は考えています。 みなさんは群数列の何が複雑なのかを分かって

等差数列 等比数列の解き方 階差数列 漸化式をスタサプ講師がわかりやすく解説 21年3月15日 エキサイトニュース 6 8

階差数列を用いて一般項を求める方法について 高校数学の美しい物語

階差数列

3分でわかる 等差数列の公式をわかりやすく 合格サプリ

等差数列の和の公式と階差数列の公式はおなじでしょうか 問 Yahoo 知恵袋

総和記号 S シグマの計算法と5つの公式 等差数列 等比数列を分かりやすく考えるコツ アタリマエ

階差数列とは 和の公式や一般項の求め方 漸化式の解き方 受験辞典

高校数学b 階差を利用する和 根号型 対数型 階乗型 受験の月

等比数列の公式まとめ 和 一般項の求め方をイチから学んでいこう 数スタ

等差数列 等比数列の一般項 和の公式 求め方を確認 Youtube

階差数列の和 三角数 父ちゃんが教えたるっ

階差数列

等比数列の一般項と和 おいしい数学

漸化式の解き方 高校生 数学 公式 家庭教師のアルファ プロ講師による高品質指導

1

等差数列の公式まとめ 一般項と和の公式を分かりやすく解説

階差数列の全てをわかりやすくまとめた 公式 漸化式 一般項の解き方 理系ラボ

中学受験 算数 等差数列 等比数列 階差数列の重点ポイントまとめ 中学受験アンサー

等差数列 等比数列の解き方 階差数列 漸化式をスタサプ講師がわかりやすく解説 高校生なう スタディサプリ進路 高校生に関するニュースを配信

無限級数 無限等比級数とは 和の公式や求め方 図形問題 受験辞典

無料プリント 等差数列の和の公式の求め方と問題の解き方 中学受験 そうちゃ式 受験算数 新1号館

階差数列の全てをわかりやすくまとめた 公式 漸化式 一般項の解き方 理系ラボ

3分でわかる 等差数列の公式をわかりやすく 合格サプリ

Sシグマの公式まとめと計算方法 数列の和の公式 理系ラボ

階差型の数列 おいしい数学

例題で学ぶ高校数学 階差数列

漸化式の意味と解き方 一般項の求め方を12パターンまとめて解説

5u8gwqhtnyjetm

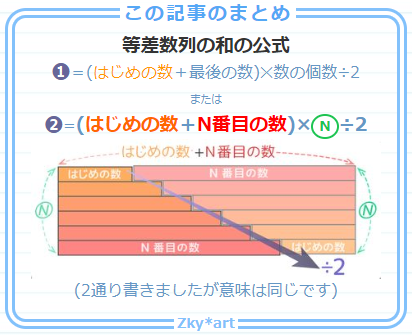
無料プリント 等差数列の和の公式の求め方と問題の解き方 中学受験 そうちゃ式 受験算数 新1号館

階差数列の考え方 高校数学の知識庫

誤答から学ぼうシリーズ 等差数列 等比数列 型の数列の和 ほのぼの数学頑張ろう

階差数列の和 について 数学b 数列

1乗和 2乗和 3乗和の公式 導出法から理解しよう

等差数列とは 和の公式や一般項の覚え方 計算問題 受験辞典

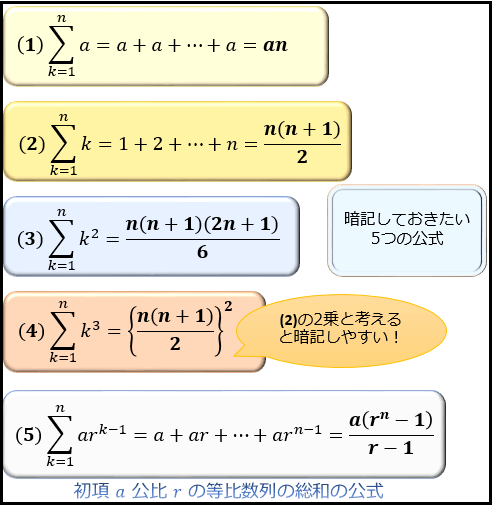
総和記号 S シグマの計算法と5つの公式 等差数列 等比数列を分かりやすく考えるコツ アタリマエ

中学受験 差 階差数列 を利用する問題の解き方 無料プリントあり そうちゃ式 受験算数 新1号館

階差数列を用いて一般項を求める方法について 高校数学の美しい物語

階差数列を利用して数列の一般項を求める問題です Clear

Sシグマの公式まとめと計算方法 数列の和の公式 理系ラボ

階差数列とは 和の公式や一般項の求め方 漸化式の解き方 受験辞典

階差数列を使った数列問題の解き方 公式を東大生がわかりやすく紹介 高校生向け受験応援メディア 受験のミカタ

高校数学b 調和数列 逆数が等差数列 の一般項 受験の月

高校数学b 等差 等比 型 2次式 等比 型の数列の和 受験の月

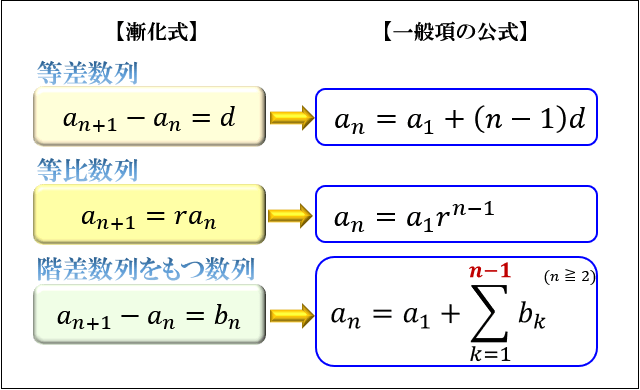
漸化式とは 等差数列 等比数列 階差数列の意味と一般項を求める公式 アタリマエ

2 5 14 41 122 365の一般項を求めよ が分かりません Clear

中学受験 算数 等差数列 等比数列 階差数列の重点ポイントまとめ 中学受験アンサー

階差数列を使った数列問題の解き方 公式を東大生がわかりやすく紹介 高校生向け受験応援メディア 受験のミカタ

等差数列の公式まとめ 一般項と和の公式を分かりやすく解説

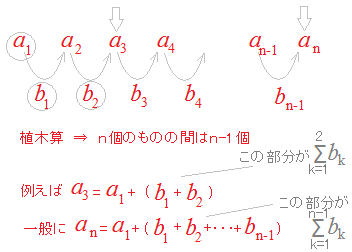
階差数列の和の考えを逆利用した数列の和の求め方 研究紀要 広島大学附属中 高等学校 47号 学内刊行物 広島大学 学術情報リポジトリ

階差数列

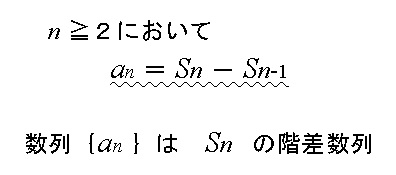
数列 の記事一覧 3 4ページ目

高校数学b 等差数列 A N の和 １ 映像授業のtry It トライイット

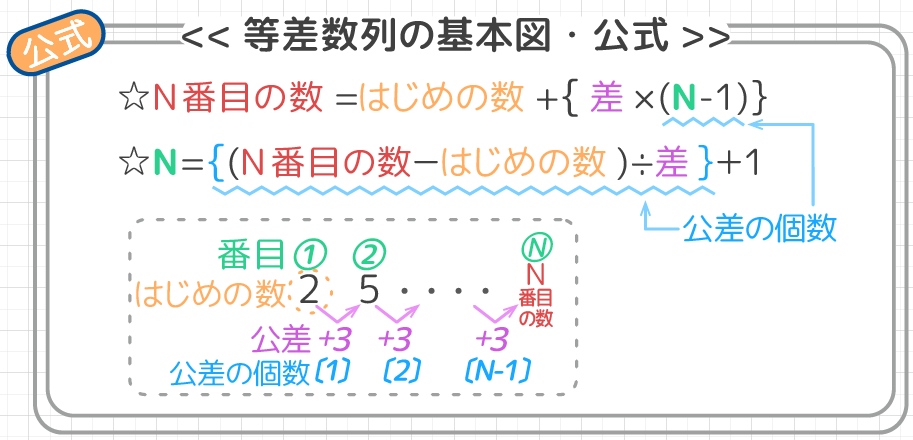
中学受験 等差 数列とは 問題と解き方まとめ 無料プリントも 小学生 そうちゃ式 受験算数 新1号館

等差数列 等比数列の解き方 階差数列 漸化式をスタサプ講師がわかりやすく解説 ガジェット通信 Getnews

Studydoctor分数の数列の和 高校数学ｂ Studydoctor

数列の基本２ 等差数列の和の公式 と 等比数列の和の公式

高校数学b S と等差 等比数列の和 練習編 映像授業のtry It トライイット

数列の基本５ 階差数列の考え方は簡単 階差数列の公式

いろいろな数列 3

階差数列の全てをわかりやすくまとめた 公式 漸化式 一般項の解き方 理系ラボ

高校数学b 等差数列の和s Nの最大 最小 受験の月

等差数列の公式まとめ 一般項と和の公式を分かりやすく解説

階差数列の全てをわかりやすくまとめた 公式 漸化式 一般項の解き方 理系ラボ

48s96ub7b0z5f Net Tousa Suuretsu

階差数列のちょっとした小手技

数列の公式はどうして成り立つの N番目の数や和の求め方を本質から理解しよう 中学受験ナビ

等比数列の一般項と和 おいしい数学

等差数列とは 和の公式や一般項の覚え方 計算問題 受験辞典

3

階差数列を使った数列問題の解き方 公式を東大生がわかりやすく紹介 高校生向け受験応援メディア 受験のミカタ

高校数学b 階差数列から一般項を求める １ 練習編 映像授業のtry It トライイット

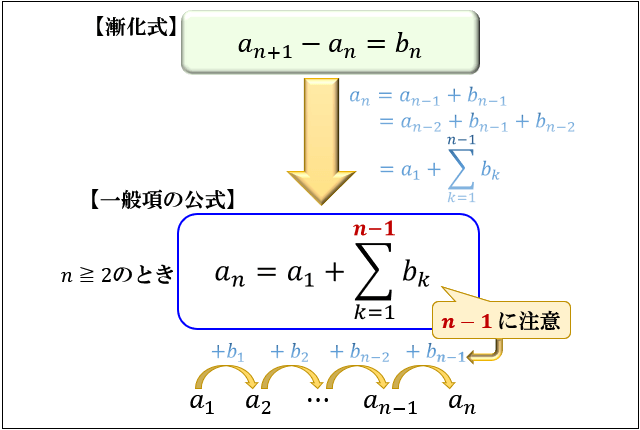
漸化式とは 等差数列 等比数列 階差数列の意味と一般項を求める公式 アタリマエ

数学用語解説 数b 数列

Q Tbn And9gcsrvyyhjkytc3 8evzp90j3lssnfzqkv5ciallewoxoskrtpciu Usqp Cau

48s96ub7b0z5f Net Syokou N Wa

階差数列とは 和の公式や一般項の求め方 漸化式の解き方 受験辞典

数列は2時間で解けるようになる 外資系コンサルタントが主夫になったら

階差数列も群数列も実は解き方は1パターン 数列の練習問題 応用編

数列と級数 京極一樹の数学塾

階差数列を使った数列問題の解き方 公式を東大生がわかりやすく紹介 高校生向け受験応援メディア 受験のミカタ

まとめ ２乗の和の公式の求め方 いろいろな方法をご紹介 ここからはじめる高校数学

等差数列 等比数列の解き方 階差数列 漸化式をスタサプ講師がわかりやすく解説 21年3月15日 エキサイトニュース 5 8

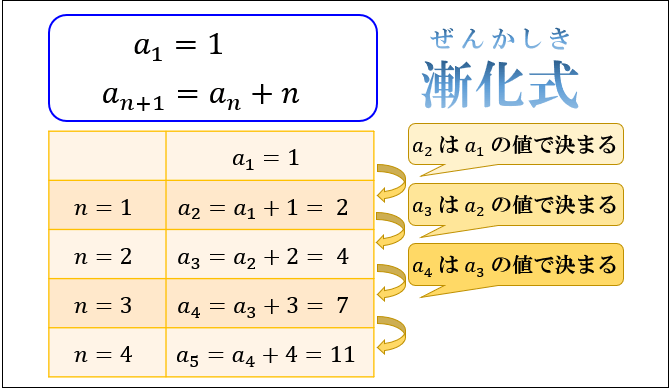
漸化式とは 等差数列 等比数列 階差数列の意味と一般項を求める公式 アタリマエ

階差数列の和 について 数学b 数列

シグマのn 1までの公式はここでまとめる 怜悧玲瓏 高校数学を天空から俯瞰する

1

階差数列の一般項の求め方を教えて下さい 1 An 1 2 5 14 Yahoo 知恵袋

高校数学b 階差数列から一般項を求める １ 映像授業のtry It トライイット

階差数列を用いて一般項を求める方法 思考力を鍛える数学

漸化式と一般項 階差形

Incoming Term: 階差数列の和の求め方,